The Cost of Robustness: Tighter Bounds on Parameter Complexity for Robust Memorization in ReLU Nets
Sep 20, 2025· ,,·
1 min read
,,·
1 min read
Yujun Kim
Chaewon Moon
Chulhee Yun
 Parameter Requirements for Robust Memorization
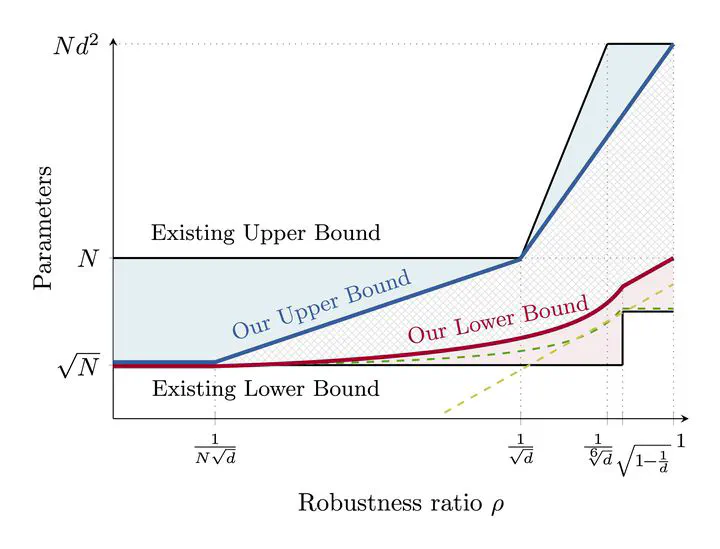
Parameter Requirements for Robust MemorizationAbstract
We study the parameter complexity of robust memorization for ReLU networks: the number of parameters required to interpolate any dataset with $\epsilon$
-separation between differently labeled points, while ensuring predictions remain consistent within a $\mu$
-ball around each training example. We establish upper and lower bounds on the parameter count as a function of the robustness ratio $\rho=\mu/\epsilon$
. Unlike prior work, we provide a fine-grained analysis across the entire range $\rho\in(0,1)$
and obtain tighter upper and lower bounds that improve upon existing results. Our findings reveal that the parameter complexity of robust memorization matches that of non-robust memorization when $\rho$
is small, but grows with increasing $\rho$
.
Type
Publication
Neural Information Processing Systems 2025
Our paper got accepted to NeurIPS 2025!
@article{kim2025cost,
title={The Cost of Robustness: Tighter Bounds on Parameter Complexity for Robust Memorization in ReLU Nets},
author={Kim, Yujun and Moon, Chaewon and Yun, Chulhee},
journal={arXiv preprint arXiv:2510.24643},
year={2025}
}